“Quadrilateral ABCD has ![]() . The perimeter of ABCD is 224 and its area is 2205. One side of ABCD has length 7. The remaining three sides have integer length. The sum of the squares of the side length of ABCD is
. The perimeter of ABCD is 224 and its area is 2205. One side of ABCD has length 7. The remaining three sides have integer length. The sum of the squares of the side length of ABCD is ![]() . What is the integer formed by the rightmost two digits of
. What is the integer formed by the rightmost two digits of ![]() ?”
?”
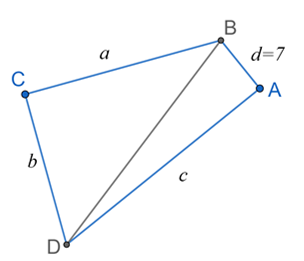
Without loss of generality, we let ![]() be four side lengths of the ABCD as shown above and
be four side lengths of the ABCD as shown above and ![]() . Then we have the following system of equations.
. Then we have the following system of equations.
![]() …(1)(by perimeter)
…(1)(by perimeter)
![]() …(2)(by area)
…(2)(by area)
![]() …(3)(by pythagorean)
…(3)(by pythagorean)
Notice that ![]() . This suggests that if we can find the value of
. This suggests that if we can find the value of ![]() , we’re done. Another notice is about the connections between the expressions
, we’re done. Another notice is about the connections between the expressions ![]() and
and ![]() . If we let
. If we let ![]() , then
, then ![]() . Also, from the equation(1), we have
. Also, from the equation(1), we have ![]() which can be substituted into the equations (2) and (3) to get a new system about
which can be substituted into the equations (2) and (3) to get a new system about ![]() and
and ![]() as follows.
as follows.
![]()
![]()
After simplifications, we have
![]()
![]()
It’s easy to solve the system and we have ![]() , and then
, and then ![]() .
.
Actually we can further solve for ![]() from
from ![]() . Finally the four side lengths are 77, 49, 91 and 7.
. Finally the four side lengths are 77, 49, 91 and 7.
Recent Comments