Problem 10 of 2000 Euclid

“An equilateral triangle ABC has side length 2. A square,PQRS, is such that P lies on AB, Q lies on BC, and R and S lie on AC as shown. The points P, Q, R, and S move so that P, Q and R always remain on the sides of the triangle and S moves from AC to AB through the interior of the triangle. If the points P, Q, R and S always form the vertices of a square, show that the path traced out by S is a straight line parallel to BC.”

The CEMC’s solution seems a little tricky. Here I want to discuss a method using analytic geometry and congruent triangles.

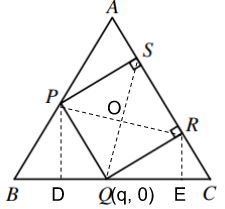
Place the equilateral triangle ABC on a coordinate plane such that $B(-1, 0), C(1, 0)$ and $A(0, \sqrt{3})$ . Let the coordinates of $Q$ be $(q, 0)$ . The problem is actually asking for showing that whatever the value of $q$ is, the $y$ -coordinate of $S$ is constant.

Let the coordinates of other points be $S(x_S, y_S)$ , $P(x_P, y_P)$ , $R(x_R, y_R)$ , $O(x_O, y_O)$ , $D(x_P, 0)$ and $E(x_R, 0)$ .

Since the point O is the midpoint of SQ and the y-coordinate of Q is always 0, we just need to show the $y_O$ is constant, by the midpoint formula of analytic geometry. Since O is also the midpoint of PR, it’s equivalent to show $y_P+y_R$ is constant.