“Points P and Q are located inside the square ABCD such that DP is parallel to QB and DP = QB = PQ. Determine the minimum possible value of ![]() .”
.”
The CEMC gave 4 solutions. Here I want to discuss a more general method using analytic geometry and trignometry. Let’s place the diagram on a coordinate plane as shown below.
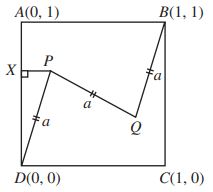
Let ![]() be the slope of the line DP. The problem is actually asking for the maximum possible value of
be the slope of the line DP. The problem is actually asking for the maximum possible value of ![]() such that the conditions “P and Q are inside ABCD”, “DP is parallel to QB” and “DP = QB = PQ” are satisfied.
such that the conditions “P and Q are inside ABCD”, “DP is parallel to QB” and “DP = QB = PQ” are satisfied.
The equation of DP is ![]() . Because DP//QB, the equation of QB will be
. Because DP//QB, the equation of QB will be ![]() . By plugging in B(1, 1), we have
. By plugging in B(1, 1), we have ![]() and
and ![]() . Because
. Because ![]() and
and ![]() , we should notice the connections between the coordinates of P and Q, that is, If we let the coordinates of P be
, we should notice the connections between the coordinates of P and Q, that is, If we let the coordinates of P be ![]() , then the coordinates of Q will be
, then the coordinates of Q will be ![]() .
.
The condition ![]() gives us the following equation:
gives us the following equation:
![]()
After calculations, we have the following quadratic equation about ![]() :
:
![]()
If the above equation has real solutions, the discriminant must be greater than or equal to 0. That is,
![]() .
.
Then we have ![]() . Therefore, the maximum possible value of
. Therefore, the maximum possible value of ![]() is
is ![]() .
.
Next we need to verify that when ![]() , P and Q are really inside the square ABCD. This can be done by solving for
, P and Q are really inside the square ABCD. This can be done by solving for ![]() and
and ![]() when
when ![]() . The result shows it is true. (The calculations are omitted here).
. The result shows it is true. (The calculations are omitted here).
Finally, we can say the maximum possible value of ![]() is
is ![]() indeed. Notice that
indeed. Notice that ![]() , therefore the minimum possible value of
, therefore the minimum possible value of ![]() is
is ![]() . Done.
. Done.
Recent Comments