How to Factor $Ax^2+Bxy+Cy^2+Dx+Ey+G$

Prerequisite: I assume you already know how to factor polynomials in the form of $ax^2+bx+c$ and $ax^2+bxy+cy^2$ . Then it’s easy to factor the polynomials in the form of $Ax^2+Bxy+Cy^2+Dx+Ey+G$ , if it is possible to do so.

Let’s see an example from CEMC courseware: https://courseware.cemc.uwaterloo.ca/8/assignments/71/9.

“The factors of $5x^2+kxy-6y^2+13x-5y+6$ are of the form $(ax+by+c)(dx+ey+f)$ , where $a, b, c, d, e, f$ are integers. Find the value of $k$ .”

The link to the CEMC’s solution is :https://courseware.cemc.uwaterloo.ca/8/assignments/71/11. Here I want to show another method. Notice that if $Ax^2+Bxy+Cy^2+Dx+Ey+G = (ax+by+c)(dx+ey+f)$ , then by distributive law we must have the following three equations satisfied at the same time.

(1) $\begin{equation*}Ax^2+Bxy+Cy^2 = (ax+by)(dx+ey)\end{equation*}$

(2) $\begin{equation*} Ax^2+Dx+G = (ax+c)(dx+f)\end{equation*}$

(3) $\begin{equation*} Cy^2+Ey+G = (by+c)(ey+f)\end{equation*}$

For that CEMC problem, we have

$5x^2+kxy-6y^2 = (ax+by)(dx+ey), and$

$5x^2+13x+6 = (5x+3)(x+2), and$

$-6y^2-5y+6 = (2y+3)(-3y+2).$

Therefore, it’s easy to see $5x^2+kxy-6y^2+13x-5y+6=(5x+2y+3)(x-3y+2)$ and $k=bd+ae=2*1+5*(-3)=-13$ .

Note: Don’t bother to multiply the two factors on the right side to find the value of $k$ . Instead, notice that $k$ is only determined by $5x*(-3y)+2y*x$ . This is also a good example for understanding distributive law and the multiplication of two polynomials.

Of course, not all polynomials in the form of $Ax^2+Bxy+Cy^2+Dx+Ey+G$ can be factored into $(ax+by+c)(dx+ey+f)$ . For the above example, if $k\neq-13$ , then $5x^2+kxy-6y^2+13x-5y+6$ can not be factored into $(ax+by+c)(dx+ey+f)$ , because we cannot find $a, b, c, d, e$ and $f$ such that the equations (1)(2) (3) are satisfed at the same time.

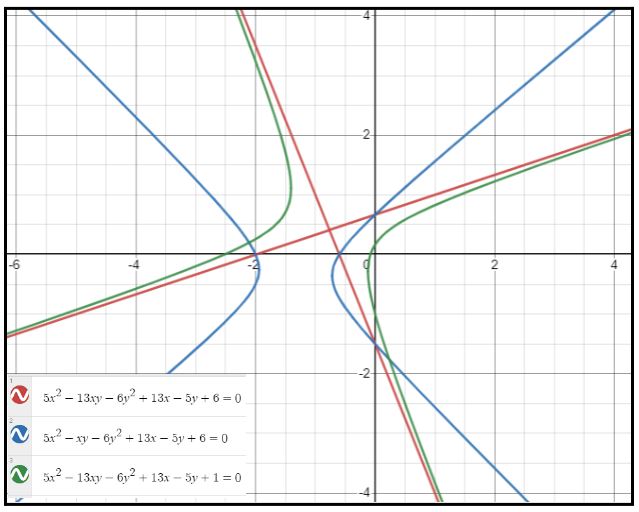
Another way to check if $Ax^2+Bxy+Cy^2+Dx+Ey+G$ can be factored into $(ax+by+c)(dx+ey+f)$ is by using a graph calculator, like Desmos, to graph $Ax^2+Bxy+Cy^2+Dx+Ey+G=0$ .