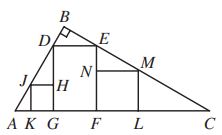
“In triangle ABC, ![]() . Rectangle DEFG is inscribed in
. Rectangle DEFG is inscribed in ![]() , as shown. Squares JKGH and
, as shown. Squares JKGH and
MLFN are inscribed in ![]() and
and ![]() , respectively. If the side length of JHGK is
, respectively. If the side length of JHGK is ![]() , the side length
, the side length
of MLFN is ![]() , and DG =
, and DG = ![]() , prove that
, prove that ![]() .”
.”
Notice that given a right triangle, the side length of the inscribed square as shown above can be expressed using two side lengths of the right triangle. Look at the following diagram.
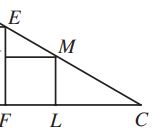
It’s easy to see ![]() , then
, then ![]() .
.
Therefore we have ![]() . This result is general. So, similarly, we can have the following equation immediately.
. This result is general. So, similarly, we can have the following equation immediately.
![]()
By ![]() , we have
, we have ![]() .
.
Therefore, ![]() and
and ![]() . By substitutions, we have the following equation:
. By substitutions, we have the following equation:
![]() . Done.
. Done.
Recent Comments