“A cube has edge length 4m. One end of a rope of length 5m is anchored to the centre of the top face of the cube. The area of the surface of the cube that can be reached by the other end of the rope is 
. What is the integer formed by the rightmost two digits of the integer closest to 
?”
Consider the net of the cube. Then it’s easy to see we just need to find the area of shaded region(light shaded plus dark shaded) in the following diagram.
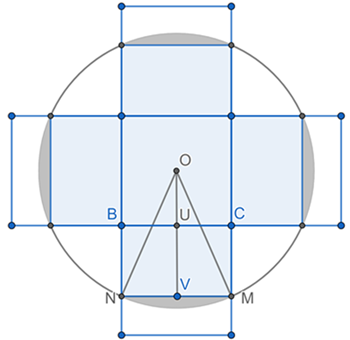
Notice that in 
. We can find the height 
. Then 
. Therefore the area of BNMC=BN*4 can be calculated.
Also notice that the area of the dark shaded circular segment=area of circular sector ONM-area of 
. Since we already know the side lengths, it’s easy to find the measure of 
by cosine law. Then we’re done.
Recent Comments